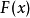设 F(x) 为函数 f(x) 的一个原函数，我们把函数 f(x) 的所有原函数 F(x)+C （C为任意常数）叫做函数 f(x) 的不定积分(indefinite integral)。

记作 \int {f(x)}dx 。 其中 \int 叫做积分号(integral sign)， f(x) 叫做被积函数(integrand)， dx 叫做积分变量， f(x)dx 叫做被积式， C 叫做积分常数，求已知函数的不定积分的过程叫做对这个函数进行积分。

由定义可知：

求函数f(x)的不定积分，就是要求出f(x)的所有的原函数，由原函数的性质可知，只要求出函数f(x)的一个原函数，再加上任意的常数C，就得到函数f(x)的不定积分。

也可以表述成,积分是微分的逆运算,即知道了导函数,求原函数。

积分的基本原理：微积分基本定理，由艾萨克·牛顿和戈特弗里德·威廉·莱布尼茨在十七世纪分别独自确立。微积分基本定理将微分和积分联系在一起，这样，通过找出一个函数的原函数，就可以方便地计算它在一个区间上的积分。积分和导数已成为高等数学中最基本的工具，并在自然科学和工程学中得到广泛运用。

积分的一个严格的数学定义由波恩哈德·黎曼给出（参见条目“黎曼积分”）。黎曼的定义运用了极限的概念，把曲边梯形设想为一系列矩形组合的极限。从十九世纪起，更高级的积分定义逐渐出现，有了对各种积分域上的各种类型的函数的积分。比如说，路径积分是多元函数的积分，积分的区间不再是一条线段（区间[a,b]），而是一条平面上或空间中的曲线段；在面积积分中，曲线被三维空间中的一个曲面代替。对微分形式的积分是微分几何中的基本概念。

对积分概念的推广来自于物理学的需要，并体现在许多重要的物理定律中，尤其是电动力学。现代的积分概念基于测度论，主要是由昂利·勒贝格建立的勒贝格积分。

众所周知，微积分的两大部分是微分与积分。微分实际上是函数的微小的增量，函数在某一点的导数值乘以自变量以这点为起点的增量，得到的就是函数的微分；它近似等于函数的实际增量（这里主要是针对一元函数而言)。而积分是已知一函数的导数，求这一函数。所以，微分与积分互为逆运算。

实际上，积分还可以分为两部分。第一种，是单纯的积分，也就是已知导数求原函数，而若F(x)的导数是f(x)，那么F(x)+C（C是常数）的导数也是f(x)，也就是说，把f(x)积分，不一定能得到F(x)，因为F(x)+C的导数也是f(x)，C是任意的常数，所以f(x)积分的结果有无数个，是不确定的，我们一律用F(x)+C代替，这就称为不定积分。

用公式表示是:

而相对于不定积分，还有定积分。所谓定积分，其形式为 \int^b_a{f(x)}dx 。之所以称其为定积分，是因为它积分后得出的值是确定的，是一个数，而不是一个函数。

定积分的定义式为：

其中， t 为分点。

直观地说，对于一个给定的正实值函数 f(x)， f(x) 在一个实数区间 [a,b] 上的定积分 \int^b_a{f(x)}dx 可以理解为在坐标平面上，由曲线 (x,f(x)) 、直线 x=a， x=b 以及 x 轴围成的曲边梯形的面积值（一种确定的实数值）。

微积分的最初发展中,定积分即黎曼积分。用自己的话来说，就是把直角坐标系上的函数的图象用平行于y轴的直线和x轴把其分割成无数个矩形，然后把某个区间[a,b]上的矩形的面积累加起来，所得到的就是这个函数的图象在区间[a,b]的面积。实际上，定积分的上下限就是区间的两个端点a、b。而实变函数中,可以利用测度论将黎曼积分推广到更加一般的情况,如勒贝格积分.

用公式表示是： \int^b_a{f(x)}dx=\lim_{n\to+\infty}{\sum_{i=0}^n{\left [ a+f(t_i)\frac{b-a}n \right]}}

我们可以看到，定积分的本质是把图象无限细分，再累加起来，而积分的本质是求一个函数的原函数。它们看起来没有任何的联系，那么为什么定积分写成积分的形式呢？

定积分与不定积分看起来风马牛不相及，但是由于一个数学上重要的理论的支撑，使得它们有了本质的密切关系。把一个图形无限细分再累加，这似乎是不可能的事情，但是由于这个理论，可以转化为计算积分。这个重要理论就是大名鼎鼎的牛顿-莱布尼兹公式，它的内容是：

如果 F'(x)=f(x)

那么 \int^b_a{f(x)}dx=F(b)-F(a)

但是这里x出现了两种意义，一是表示积分上限，二是表示被积函数的自变量，但定积分中被积函数的自变量取一个定值是没意义的。虽然这种写法是可以的，但习惯上常把被积函数的自变量改成别的字母如t，这样意义就非常清楚了：

牛顿-莱布尼兹公式用文字表述，就是说一个定积分式的值，就是上限在原函数的值与下限在原函数的值的差。

正这个理论揭示了积分与黎曼积分本质的联系，可见其在微积分学乃至整个高等数学上的重要地位，因此，牛顿-莱布尼兹公式也被称作微积分基本定理。

积分是微分的逆运算，即知道了函数的导函数，反求原函数。在应用上，积分作用不仅如此，它被大量应用于求和，通俗的说是求曲边三角形的面积，这巧妙的求解方法是积分特殊的性质决定的。

一个函数的不定积分（亦称原函数）指另一族函数，这一族函数的导函数恰为前一函数。

其中：[F(x)+C]'=f(x)

一个实变函数在区间[a,b]上的定积分，是一个实数。它等于该函数的一个原函数在b的值减去在a的值。

积分 integral 从不同的问题抽象出来的两个数学概念。定积分和不定积分的统称。不定积分是为解决求导和微分的逆运算而提出的。例如：已知定义在区间I上的函数f(x)，求一条曲线y=F(x)，x\in I，使得它在每一点的切线斜率为F'(x)=f(x)。函数f(x)的不定积分是f(x)的全体原函数（见原函数），记作 。如果F(x)是f(x)的一个原函数，则 ，其中C为任意常数。例如， 定积分是以平面图形的面积问题引出的。y=f(x)为定义在[a,b]上的函数，为求由x=a，x=b ，y=0和y=f(x)所围图形的面积S，采用古希腊人的穷竭法，先在小范围内以直代曲，求出S的近似值，再取极限得到所求面积S，为此，先将[a,b]分成n等分：a=x_0 < x_1\ldots x_n=b，取\zeta i\in[x_i-1,x_i]，记\Delta x_i=x_i-x_{i-1}，则pn为S的近似值，当n\to+\infty，pn的极限应可作为面积S。把这一类问题的思想方法抽象出来，便得定积分的概念：对于定义在[a,b]上的函数y=f(x)，作分划a=x_0<\ldots<x_n=b，若存在一个与分划及\zeta i\in[x_{i-1},x_i]的取法都无关的常数I，使得,其中则称I为f(x)在[a,b]上的定积分，表为即 称[a,b]为积分区间，f(x)为被积函数，a，b分别称为积分的上限和下限。当f(x)的原函数存在时，定积分的计算可转化为求f(x)的不定积分：这是c牛顿莱布尼兹公式。

以上讲的是传统意义上的积分也即黎曼积分。